The Nature of Radiation

All objects above the temperature of absolute zero (-273.15° Celsius) radiate energy to their surrounding environment. This energy, or radiation, is emitted as electromagnetic waves that travel at the speed of light. Many different types of radiation have been identified. Each of these types is defined by its wavelength. The wavelength of electromagnetic radiation can vary from being infinitely short to infinitely long (Figure 6f-1).

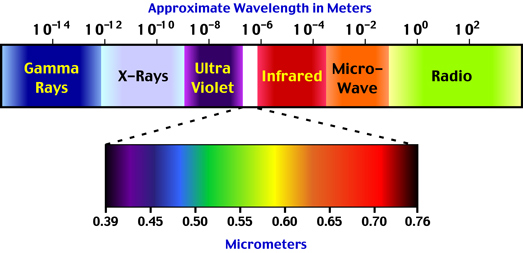
Visible light is a form of electromagnetic radiation that can be perceived by our eyes. Light has a wavelength of between 0.40 to 0.71 micrometers (µm). Figure 6f-1 illustrates that various spectral color bands that make up light. The Sun emits only a portion (44 %) of its radiation in zone. Solar radiation spans a spectrum from approximately 0.1 to 4.0 micrometers. The band from 0.1 to 0.4 micrometers is called ultraviolet radiation. About 7% of the Sun's emission is in this wavelength band. About 48% of the Sun's radiation falls in the region between 0.71 to 4.0 micrometers. This band is called the near (0.71 to 1.5 micrometers) and far infrared (1.5 to 4.0 micrometers). 

The amount of electromagnetic radiation emitted by a body is directly related to its temperature. If the body is a perfect emitter (black body), the amount of radiation given off is proportional to the 4th power of its temperature as measured in Kelvin units. This natural phenomenon is described by the Stefan-Boltzmann Law. The following simple equation describes this law mathematically:

According to the Stephan-Boltzmann equation, a small increase in the temperature of a radiating body results in a large amount of additional radiation being emitted.

In general, good emitters of radiation are also good absorbers of radiation at specific wavelength bands. This is especially true of gases and is responsible for the Earth's greenhouse effect. Likewise, weak emitters of radiation are also weak absorbers of radiation at specific wavelength bands. This fact is referred to as Kirchhoff's Law. Some objects in nature have almost completely perfect abilities to absorb and emit radiation. We call these objects black bodies. The radiation characteristics of the Sun and the Earth are very close to being black bodies.

The wavelength of maximum emission of any body is inversely proportional to its absolute temperature. Thus, the higher the temperature, the shorter the wavelength of maximum emission. This phenomenon is often called Wien's Law. The following equation describes this law:

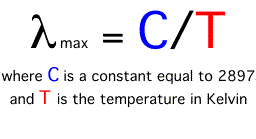
Wien's law suggests that as the temperature of a body increases, the wavelength of maximum emission becomes smaller. According to the above equation the wavelength of maximum emission for the Sun (5800 Kelvins) is about 0.5 micrometers, while the wavelength of maximum emission for the Earth (288 Kelvins) is approximately 10.0 micrometers.

A graph that describes the quantity of radiation that is emitted from a body at particular wavelengths is commonly called a spectrum. The following two graphs describe the spectrums for the Sun and Earth.

SUN

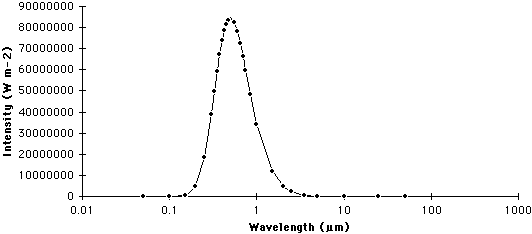
Figure 6f-2: Spectrum of the Sun. The Sun emits most of its radiation in a wavelength band between 0.1 and 4.0 micrometers (µm).

EARTH

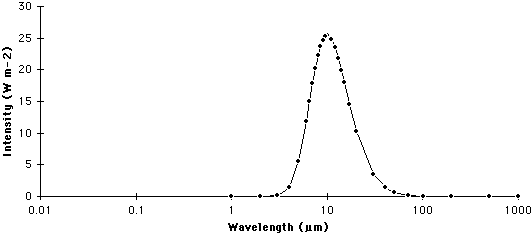
Figure 6f-3: Spectrum of the Earth. The Earth emits most of its radiation in a wavelength band between 0.5 and 30.0 micrometers (µm).

The above graphs illustrate two important points concerning the relationship between the temperature of a body and its emissions of electromagnetic radiation:

1. The amount of radiation emitted from a body increases exponentially with a linear rise in temperature (see above Stephan-Boltzmann's Law).
2. The average wavelength of electromagnetic emissions becomes shorter with increasing temperature (see above Wien's Law).

Finally, the amount of radiation passing through a specific area is inversely proportional to the square of the distance of that area from the energy source. This phenomenon is called the Inverse Square Law. Using this law we can model the effect that distance traveled has on the intensity of emitted radiation from a body like the Sun. Figure 6f-4 suggests that the intensity of radiation emitted by a body quickly diminishes with distance in a nonlinear fashion.

Figure 6f-4: Diagram illustrating the diffusion of radiation due to the Inverse Square Law.

Mathematically, the Inverse Square Law is described by the equation:

Intensity = I/d²

where I is the intensity of the radiation at 1d (see above diagram) and d is the distance traveled.

Let us try this equation out. For example, what would be the intensity of emitted radiation traveling two units of distance if the intensity at 1d = 90,000 units?

Intensity = 90,000/2²

Intensity = 90,000/4

Intensity = 22,500 units

 

What would be the intensity of emitted radiation traveling three units of distance if the intensity at 1d = 90,000 units?

Intensity = 90,000/3²

Intensity = 90,000/9

Intensity = 10,000 units

 

What would be the intensity of emitted radiation traveling four units of distance if the intensity at 1d = 90,000 units?

Intensity = 90,000/4²

Intensity = 90,000/16

Intensity = 5625 units

Note that the decrease in intensity with distance is not linear when graphed (Figure 6f-5)!

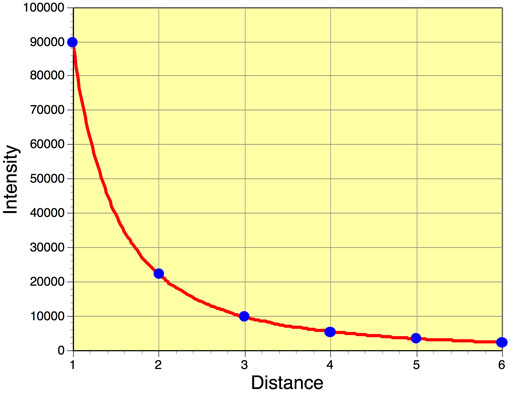
Figure 6f-5: Reduction in intensity of radiation with distance traveled.